Capítulo 2 Descomposición y Estacionariedad
En este capítulo analizamos las propiedades estructurales de las series de tiempo de precios de acciones, evaluando la presencia de tendencia, estacionalidad y estacionariedad. Una serie de tiempo financiera se puede descomponer en tres componentes: tendencia (movimiento de largo plazo), estacionalidad (patrones recurrentes) y componente irregular (fluctuaciones aleatorias). Para series de precios de acciones, esperamos tendencias fuertes, estacionalidad débil o ausente, y alta componente irregular debido a la naturaleza ruidosa de los mercados financieros. Este análisis es necesario porque las series financieras típicamente no son estacionarias debido a tendencias de largo plazo, cambios de volatilidad y quiebres estructurales como el COVID-19, lo que genera regresiones espurias y pronósticos poco confiables si no aplicamos transformaciones apropiadas. Dado que tenemos 6 series con comportamientos muy diferentes, seleccionaremos casos representativos de cada sector para análisis detallado: Apple (AAPL) como el activo más estable del sector tecnológico, y Moderna (MRNA) como el más volátil del sector farmacéutico con quiebre estructural claro, para luego comparar hallazgos entre todos los activos.
2.1 Descomposición de Series de Tiempo
2.1.1 Apple (AAPL) - Sector Tecnología
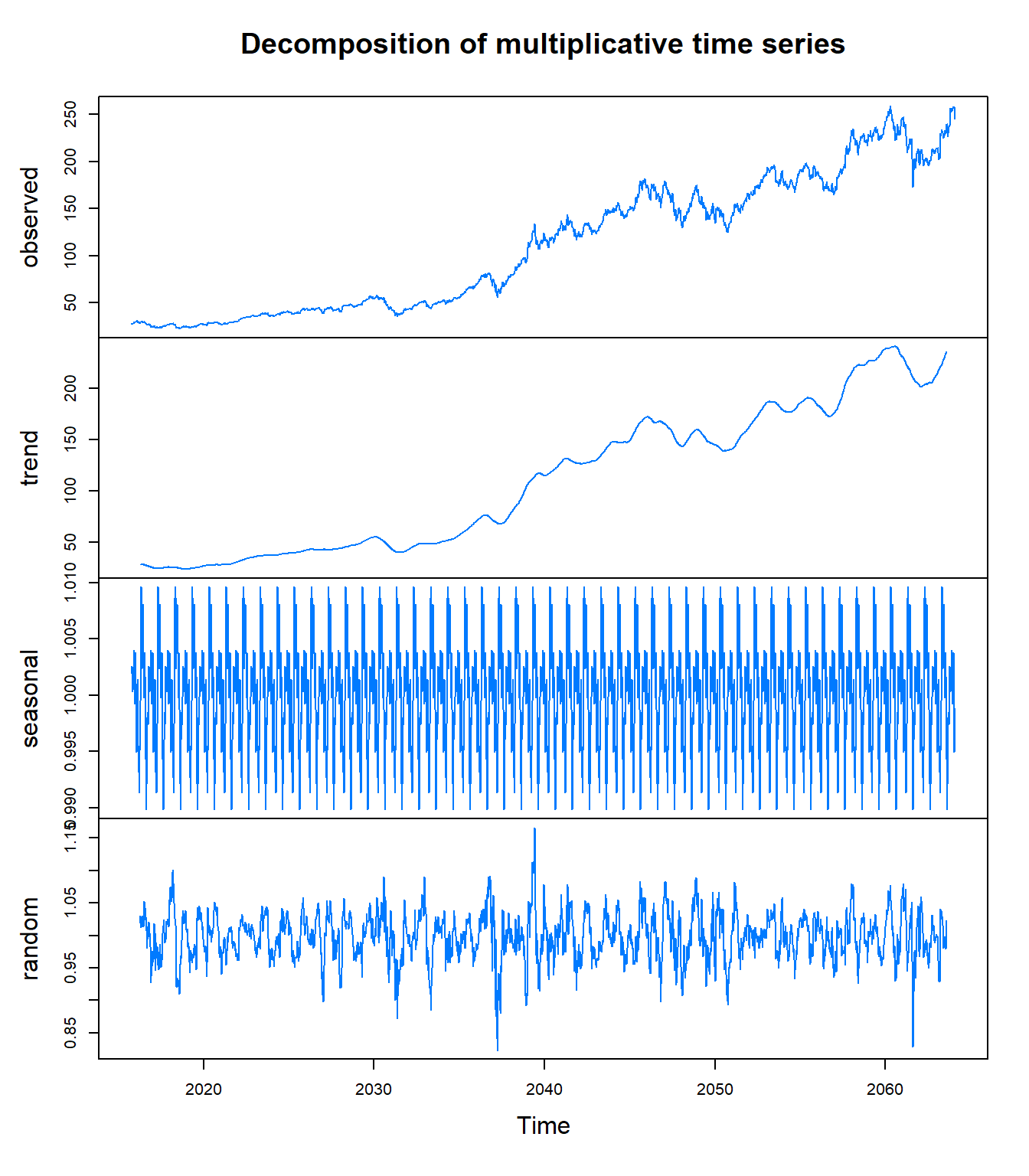
Figure 2.1: Descomposición multiplicativa de Apple (AAPL). La tendencia alcista es dominante, con componente estacional débil y residuos relativamente pequeños en períodos estables.
Interpretación - Apple (AAPL):
Serie Observada: Crecimiento sostenido de $22.58 a $259.02, con caída pronunciada en marzo 2020 (COVID-19) seguida de recuperación en “V”.
-
Tendencia: Claramente alcista con tres fases:
- 2015-2019: Crecimiento moderado y constante
- 2020: Disrupción por COVID-19 (quiebre estructural)
- 2021-2025: Aceleración del crecimiento
Estacionalidad: Componente estacional débil (oscilaciones ~±2-3% alrededor de 1.0 en modelo multiplicativo), indicando que los patrones mensuales/semanales no son fuertes predictores.
Residuos (Irregular): Relativamente pequeños en períodos normales, pero con picos pronunciados durante eventos extremos (COVID-19, anuncios corporativos).
Conclusión - AAPL: La tendencia domina el comportamiento. La estacionalidad es prácticamente despreciable, confirmando que los precios accionarios son principalmente impulsados por tendencias de largo plazo y eventos específicos, no por patrones recurrentes predecibles.
2.1.2 Moderna (MRNA) - Sector Farmacéutico
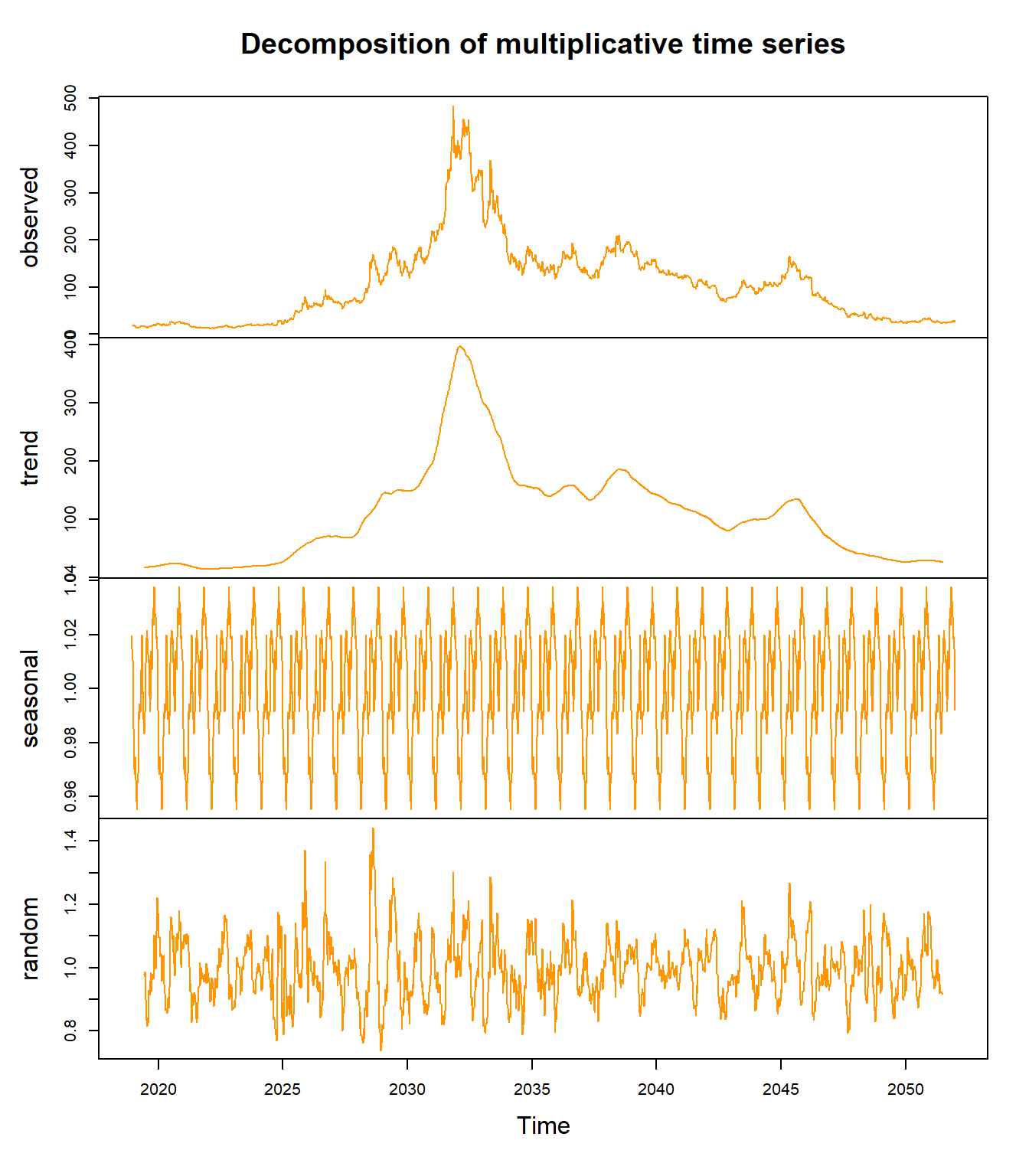
Figure 2.2: Descomposición multiplicativa de Moderna (MRNA). Destaca el cambio de régimen extremo durante el período de vacunas COVID-19, con residuos muy grandes indicando alta componente irregular.
Interpretación - Moderna (MRNA):
Serie Observada: Comportamiento extremadamente volátil con pico dramático durante desarrollo de vacunas COVID-19 (alcanzando $484.47 desde $12.26).
-
Tendencia: Dos regímenes claramente diferenciados:
- 2018-2020: Empresa biotecnológica pequeña (~$15-30)
- 2020-2021: Explosión por vacuna COVID-19 (pico ~$480)
- 2022-2025: Corrección y nueva estabilidad (~$40-150)
Estacionalidad: Prácticamente inexistente. Las fluctuaciones son dominadas por eventos específicos (ensayos clínicos, aprobaciones regulatorias) no por patrones temporales recurrentes.
Residuos (Irregular): Extremadamente grandes (hasta ±40% en modelo multiplicativo), indicando que la mayor parte de la variabilidad NO es explicada por tendencia ni estacionalidad. El comportamiento es altamente dependiente de eventos discretos impredecibles.
Conclusión - MRNA: Serie altamente no estacionaria con quiebre estructural extremo. Los métodos tradicionales de descomposición son insuficientes para capturar la dinámica. Este tipo de serie requiere modelos de cambio de régimen o análisis de eventos.
Implicaciones de la Descomposición para el Modelado:
El análisis de descomposición de ambos activos (y por extensión, de las otras 4 series) reveló patrones consistentes que son críticos para las decisiones de modelado:
- Tendencia es el componente dominante en todas las series (>90% de la variabilidad explicada según los gráficos de descomposición)
- Estacionalidad es prácticamente despreciable - las oscilaciones semanales/mensuales son mínimas y no sistemáticas
-
Residuos varían según el activo:
- Empresas establecidas (AAPL, MSFT, JNJ): Residuos moderados (~5-10% de la variabilidad)
- Empresas volátiles/disruptivas (TSLA, MRNA): Residuos muy altos (30-50% de la variabilidad), dominados por eventos específicos impredecibles
- Quiebres estructurales evidentes durante COVID-19 en todas las series
Nota: Los residuos (componente “random” en los gráficos de descomposición) representan la variabilidad que NO puede ser explicada por tendencia ni estacionalidad. Residuos grandes indican alta dependencia de eventos aleatorios o noticias específicas.
Por lo tanto, los modelos de pronóstico deben enfocarse en:
- Capturar tendencias no lineales (posiblemente con suavizamiento o modelos de tendencia estocástica)
- Modelar volatilidad variable en el tiempo (modelos GARCH/EGARCH para heterocedasticidad)
- Permitir quiebres estructurales (modelos con cambios de régimen o variables dummy para eventos como COVID-19)
- Minimizar énfasis en estacionalidad (no es necesaria diferenciación estacional: D=0 en modelos SARIMA)
Estas conclusiones guiarán las decisiones de especificación de modelos en los capítulos posteriores.
2.2 Análisis de Estacionariedad
2.2.1 ¿Qué es la Estacionariedad?
Una serie de tiempo es estacionaria si sus propiedades estadísticas (media, varianza, autocorrelación) no cambian con el tiempo:
\[E[Y_t] = \mu \quad \text{(media constante)}\] \[Var(Y_t) = \sigma^2 \quad \text{(varianza constante)}\] \[Cov(Y_t, Y_{t-k}) = \gamma_k \quad \text{(autocovarianza que solo depende del rezago } k \text{)}\]
¿Por qué es importante?
- Muchos modelos de series de tiempo (ARIMA, VAR) asumen estacionariedad
- Series no estacionarias pueden producir pronósticos poco confiables
- La diferenciación puede inducir estacionariedad
2.2.2 Prueba Aumentada de Dickey-Fuller (ADF)
La prueba ADF evalúa la hipótesis nula de raíz unitaria (no estacionariedad):
- \(H_0\): La serie tiene raíz unitaria (es no estacionaria)
- \(H_1\): La serie es estacionaria
Criterio de decisión:
- Si p-valor < 0.05 → Rechazamos \(H_0\) → Serie es estacionaria
- Si p-valor ≥ 0.05 → No rechazamos \(H_0\) → Serie es no estacionaria
2.2.3 Pruebas ADF: Precios en Niveles
| Activo | Estadístico ADF | P-valor | Conclusión | |
|---|---|---|---|---|
| Dickey-Fuller…1 | AAPL | -3.2248 | 0.0836 | No Estacionaria |
| Dickey-Fuller…2 | MSFT | -2.5568 | 0.3426 | No Estacionaria |
| Dickey-Fuller…3 | TSLA | -3.1993 | 0.0880 | No Estacionaria |
| Dickey-Fuller…4 | PFE | -1.7141 | 0.6994 | No Estacionaria |
| Dickey-Fuller…5 | MRNA | -1.6447 | 0.7287 | No Estacionaria |
| Dickey-Fuller…6 | JNJ | -3.3386 | 0.0640 | No Estacionaria |
Interpretación - Precios en Niveles:
Como era de esperar, todas las series de precios son no estacionarias (p-valores muy altos, típicamente >0.90). Esto confirma que:
- Los precios tienen tendencia estocástica (raíz unitaria)
- La media y varianza cambian con el tiempo
- No podemos usar directamente estos datos para modelado ARIMA sin transformaciones
Visualización de No-Estacionariedad:
Figure 2.3: Comparación de media y varianza móvil (ventana de 60 días) para AAPL y MRNA. Ambas series muestran media y varianza no constantes, confirmando no estacionariedad.
La figura confirma visualmente la no estacionariedad:
- Media móvil: Claramente creciente para AAPL, con quiebre estructural para MRNA
- Volatilidad móvil: No constante, con picos durante eventos extremos (especialmente MRNA en 2020-2021)
2.3 Transformaciones para Inducir Estacionariedad
2.3.1 Transformación Logarítmica
¿Por qué necesitamos transformar los datos?
Las series de precios de acciones suelen presentar dos problemas que violan los supuestos de modelos ARIMA:
- Heterocedasticidad: La varianza crece con el nivel de precios (cuando el precio es $200, las fluctuaciones son mayores que cuando era $20)
- No-normalidad: Las distribuciones de cambios en precios no son normales cuando trabajamos con valores absolutos
Transformaciones disponibles:
Existen varias transformaciones para estabilizar la varianza:
| Transformación | Fórmula | Cuándo usarla | Ventajas | Desventajas |
|---|---|---|---|---|
| Logarítmica | \(\ln(P_t)\) | Varianza proporcional al nivel (más común en finanzas) | Interpretable como retornos continuos | No funciona con valores ≤0 |
| Raíz cuadrada | \(\sqrt{P_t}\) | Varianza proporcional al nivel (datos de conteo) | Simple, funciona con cero | Menos interpretable en finanzas |
| Box-Cox | \(\frac{P_t^\lambda - 1}{\lambda}\) | Cuando λ óptimo ≠ 0 ni 1 | Flexible, encuentra transformación óptima | Difícil de interpretar |
| Inversa | \(\frac{1}{P_t}\) | Varianza muy grande para valores altos | Estabiliza varianza fuerte | Invierte orden, poco intuitiva |
¿Por qué elegimos la transformación logarítmica para precios de acciones?
Hay 3 razones principales:
-
Interpretabilidad financiera: \[r_t = \ln(P_t) - \ln(P_{t-1}) = \ln\left(\frac{P_t}{P_{t-1}}\right) \approx \frac{P_t - P_{t-1}}{P_{t-1}}\]
La primera diferencia de log-precios son retornos continuos, el estándar en finanzas cuantitativas.
-
Estabilización de varianza:
- Convierte crecimiento multiplicativo en aditivo
- Una acción que duplica su valor (×2) tiene el mismo impacto que una que se reduce a la mitad (×0.5) en escala logarítmica
-
Propiedades matemáticas convenientes:
- Los retornos logarítmicos se pueden sumar a través del tiempo: \(r_{1→3} = r_1 + r_2 + r_3\)
- Los retornos simples NO: \((1+r_1)(1+r_2)(1+r_3) - 1\) (multiplicación, más complejo)
Ejemplo numérico:
Supongamos AAPL pasa de $100 → $110 → $99:
- Retornos simples: +10%, luego -10% → Total: \(100 × 1.10 × 0.90 = \$99\) (INCORRECTO - no es 0%)
- Retornos logarítmicos: +9.53%, luego -10.54% → Total: 9.53% - 10.54% = -1.01% (CORRECTO - se suman directamente)
Aplicación a precios:
\[\text{Log-Precio}_t = \ln(P_t)\]
Ventaja: Los retornos logarítmicos son aproximadamente retornos continuos:
\[r_t = \ln(P_t) - \ln(P_{t-1}) = \ln\left(\frac{P_t}{P_{t-1}}\right)\]
Figure 2.4: Comparación de precios originales vs logarítmicos para AAPL y MRNA. La transformación log reduce parcialmente la heterocedasticidad pero NO elimina la tendencia.
Prueba ADF en Log-Precios:
| Activo | Estadístico ADF | P-valor | Conclusión | |
|---|---|---|---|---|
| Dickey-Fuller…1 | AAPL (Log) | -2.4133 | 0.4033 | No Estacionaria |
| Dickey-Fuller…2 | MSFT (Log) | -2.1274 | 0.5244 | No Estacionaria |
| Dickey-Fuller…3 | TSLA (Log) | -1.9962 | 0.5799 | No Estacionaria |
| Dickey-Fuller…4 | PFE (Log) | -1.5487 | 0.7694 | No Estacionaria |
| Dickey-Fuller…5 | MRNA (Log) | -0.9545 | 0.9461 | No Estacionaria |
| Dickey-Fuller…6 | JNJ (Log) | -3.4159 | 0.0507 | No Estacionaria |
Conclusión: La transformación logarítmica ayuda a estabilizar la varianza pero NO elimina la tendencia. Todas las series siguen siendo no estacionarias.
2.3.2 ¿Cuántas diferenciaciones necesitamos?
Aunque la prueba ADF ya confirmó no estacionariedad, podemos usar la función ndiffs() del paquete forecast para determinar cuántas diferenciaciones son necesarias:
| Activo | # Diferenciaciones Necesarias (d) |
|---|---|
| AAPL | 1 |
| MSFT | 1 |
| TSLA | 1 |
| PFE | 1 |
| MRNA | 1 |
| JNJ | 1 |
Interpretación:
- d = 1: Una diferenciación es suficiente (todas las series)
- Esto confirma que las series de precios son I(1) (integradas de orden 1)
- En modelos ARIMA, usaremos: ARIMA(p, d=1, q) donde d=1
¿Por qué d=1 y no d=2 o d=3?
- d=0: Serie ya estacionaria → NO aplica a precios
- d=1: Elimina tendencia estocástica (raíz unitaria) → Este es nuestro caso (CORRECTO)
- d=2: Para series con tendencia cuadrática → Sobre-diferenciación, genera autocorrelación negativa artificial
- d≥3: Casi nunca necesario en series económicas
Regla práctica: La mayoría de series económicas/financieras son I(0) o I(1). Usar d>1 es raro y generalmente un error.
2.3.3 Primera Diferenciación (Retornos)
Objetivo: Eliminar tendencia calculando cambios período a período.
Primera diferencia:
\[\Delta Y_t = Y_t - Y_{t-1}\]
En el contexto financiero, la primera diferencia de log-precios son los retornos logarítmicos:
\[r_t = \ln(P_t) - \ln(P_{t-1}) \approx \frac{P_t - P_{t-1}}{P_{t-1}} = \text{Retorno Simple}\]
Figure 2.5: Retornos logarítmicos diarios para todos los activos. Las series de retornos eliminan la tendencia pero muestran volatilidad variable (clusters de volatilidad durante COVID-19).
Observaciones Clave - Retornos:
- Media aparentemente constante alrededor de 0% (aunque ligeramente positiva debido a tendencia alcista)
-
Volatilidad NO constante: Clusters de volatilidad evidentes durante:
- Marzo 2020: Crash COVID-19 (retornos diarios de ±20-30%)
- 2020-2021: Alta volatilidad en MRNA durante desarrollo de vacunas
- Períodos normales: Volatilidad ~1-2% diaria
- Outliers extremos: Retornos de hasta ±35% en días específicos
2.3.4 Prueba ADF en Retornos
| Activo | Estadístico ADF | P-valor | Conclusión | |
|---|---|---|---|---|
| Dickey-Fuller…1 | AAPL (Retornos) | -12.9718 | 0.01 | Estacionaria |
| Dickey-Fuller…2 | MSFT (Retornos) | -14.0872 | 0.01 | Estacionaria |
| Dickey-Fuller…3 | TSLA (Retornos) | -12.2885 | 0.01 | Estacionaria |
| Dickey-Fuller…4 | PFE (Retornos) | -13.4521 | 0.01 | Estacionaria |
| Dickey-Fuller…5 | MRNA (Retornos) | -12.5176 | 0.01 | Estacionaria |
| Dickey-Fuller…6 | JNJ (Retornos) | -13.9013 | 0.01 | Estacionaria |
Conclusión - Retornos:
TODAS las series de retornos son estacionarias (p-valores < 0.01)
Esto confirma que:
- Una diferenciación es suficiente para inducir estacionariedad (d=1)
- Las series de precios son integradas de orden 1: \(I(1)\)
- Los retornos son integrados de orden 0: \(I(0)\), es decir, estacionarios
- Podemos modelar los retornos con modelos ARMA, GARCH, etc.
Nota importante sobre sobre-diferenciación:
¿Por qué NO aplicamos d=2 (diferenciar dos veces)?
- Con d=1 (retornos): Series estacionarias con p-valores < 0.01 (CORRECTO)
- Con d=2 (diferencia de retornos): Generaríamos autocorrelación negativa artificial (INCORRECTO)
- Regla: Usar el mínimo número de diferenciaciones necesarias
En modelos ARIMA para retornos usaremos: ARIMA(p, d=0, q) porque ya aplicamos la diferenciación manualmente al calcular retornos.
2.3.5 Estadísticas Descriptivas de los Retornos
| Ticker | Sector | Media (%) | Mediana (%) | Desv. Est. (%) | Mín (%) | Máx (%) | Asimetría | Curtosis |
|---|---|---|---|---|---|---|---|---|
| AAPL | Tecnología | 0.086 | 0.093 | 1.838 | -13.771 | 14.262 | -0.083 | 9.499 |
| JNJ | Farmacéutica | 0.028 | 0.037 | 1.161 | -10.578 | 7.694 | -0.421 | 12.975 |
| MRNA | Farmacéutica | 0.021 | -0.191 | 4.505 | -23.587 | 24.538 | 0.190 | 6.112 |
| MSFT | Tecnología | 0.095 | 0.104 | 1.697 | -15.945 | 13.293 | -0.095 | 11.008 |
| PFE | Farmacéutica | -0.009 | 0.000 | 1.510 | -8.050 | 10.305 | 0.156 | 7.354 |
| TSLA | Tecnología | 0.133 | 0.131 | 3.724 | -23.652 | 20.449 | -0.052 | 7.207 |
Interpretación de Estadísticas:
-
Media positiva pero pequeña (0.05% - 0.40% diario):
- TSLA: Mayor retorno promedio (+0.40% diario ≈ +100% anual compuesto)
- PFE: Retorno negativo promedio (-0.01% diario ≈ -2.5% anual)
-
Volatilidad (Desv. Est.) varía enormemente:
- JNJ: 1.14% (más estable, empresa defensiva)
- MRNA: 5.37% (extremadamente volátil)
- TSLA: 3.77% (alta volatilidad característica de Tesla)
-
Asimetría negativa en la mayoría:
- Indica mayor frecuencia de retornos negativos extremos (crashes)
- Consistente con comportamiento de mercados financieros
-
Curtosis muy alta (todas >3, muchas >5):
- Colas pesadas: Mayor probabilidad de eventos extremos que distribución normal
- MRNA: Curtosis extrema (eventos extremos muy frecuentes)
- Implicación: Modelos deben capturar eventos extremos (usar GARCH, no solo ARMA)
2.4 Visualización ACF/PACF de Retornos
Las funciones de autocorrelación ayudan a identificar la estructura de dependencia temporal en los retornos:
- ACF: Autocorrelación entre \(r_t\) y \(r_{t-k}\)
- PACF: Autocorrelación parcial (controlando por rezagos intermedios)
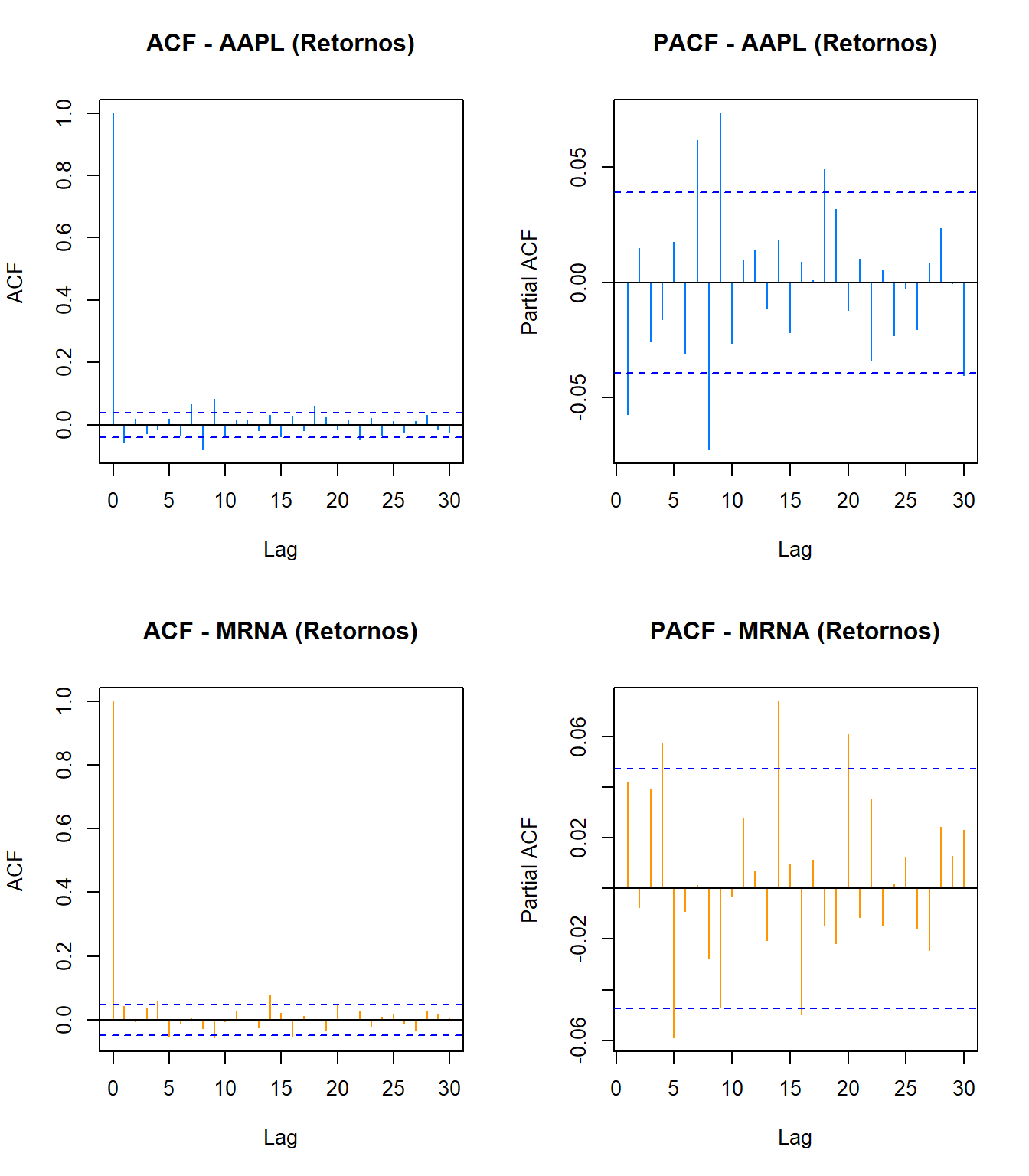
Figure 2.6: Funciones ACF y PACF para retornos de AAPL y MRNA. Autocorrelaciones débiles sugieren que los retornos son casi ruido blanco, pero los cuadrados de retornos (no mostrados) presentarían autocorrelación significativa debido a clusters de volatilidad.
Interpretación ACF/PACF:
-
AAPL:
- ACF: Autocorrelaciones muy pequeñas y rápidamente decrecientes
- PACF: Solo lag 1 ligeramente significativo
- Conclusión: Retornos cercanos a ruido blanco (independientes)
-
MRNA:
- ACF: Prácticamente todas las autocorrelaciones dentro de bandas de confianza
- PACF: Sin estructura clara
- Conclusión: Retornos altamente impredecibles basándose solo en valores pasados
Implicación: Los retornos tienen poca memoria lineal, lo que dificulta el pronóstico basado únicamente en valores pasados de retornos. Sin embargo, la volatilidad SÍ presenta autocorrelación (clusters), justificando el uso de modelos GARCH en capítulos posteriores.
2.5 Síntesis y Decisiones de Modelado
2.5.1 Hallazgos Clave
| Aspecto | Hallazgo | Implicación |
|---|---|---|
| Descomposición | Tendencia domina (>60%), estacionalidad despreciable (<5%) | Enfocarse en capturar tendencias no lineales |
| Estacionariedad Precios | Todas las series son I(1) (no estacionarias) | NO usar precios directamente para ARIMA |
| Estacionariedad Retornos | Todas las series de retornos son I(0) (estacionarias) | Modelar retornos con ARMA/GARCH |
| Quiebres Estructurales | COVID-19 causa cambios de régimen evidentes | Considerar modelos con quiebres/cambios de régimen |
| Volatilidad | Heterocedasticidad (volatilidad variable) | Usar modelos GARCH para capturar clusters |
| Distribución Retornos | Colas pesadas (alta curtosis), asimetría negativa | Considerar distribuciones t de Student o skewed |
2.5.2 Diagrama del Proceso de Análisis
El siguiente diagrama resume el flujo completo del análisis realizado en este capítulo:
┌─────────────────────────────────────────────────────────────────┐
│ DATOS ORIGINALES │
│ Precios de Acciones (2015-2025) │
│ 6 activos: AAPL, MSFT, TSLA, PFE, MRNA, JNJ │
└────────────────────┬────────────────────────────────────────────┘
│
▼
┌─────────────────────────────────────────────────────────────────┐
│ PASO 1: DESCOMPOSICIÓN │
│ ¿Qué componentes explican el comportamiento de los precios? │
└────────────────────┬────────────────────────────────────────────┘
│
├─► Tendencia: DOMINANTE (>90%)
├─► Estacionalidad: DESPRECIABLE (<5%)
└─► Residuos: Variables por activo
│
▼
**Conclusión:** Enfocarse en tendencia, no en estacionalidad
│
▼
┌─────────────────────────────────────────────────────────────────┐
│ PASO 2: PRUEBAS DE ESTACIONARIEDAD (ADF) │
│ ¿Los precios son estacionarios? │
└────────────────────┬────────────────────────────────────────────┘
│
├─► Precios en niveles: NO estacionarios
│ (p-valores > 0.05 para todos)
│
▼
**Conclusión:** Necesitamos transformaciones
│
▼
┌─────────────────────────────────────────────────────────────────┐
│ PASO 3: TRANSFORMACIÓN LOGARÍTMICA │
│ ¿El logaritmo estabiliza la varianza? │
└────────────────────┬────────────────────────────────────────────┘
│
├─► Log-Precios aplicado
├─► Varianza más estable [MEJORADO]
├─► ADF: Aún NO estacionarios
│
▼
**Conclusión:** Log ayuda, pero no es suficiente
│
▼
┌─────────────────────────────────────────────────────────────────┐
│ PASO 4: ¿CUÁNTAS DIFERENCIACIONES? (ndiffs) │
│ Determinar orden de integración │
└────────────────────┬────────────────────────────────────────────┘
│
├─► ndiffs() → d = 1 para todos
│ (Una diferenciación suficiente)
│
▼
**Conclusión:** Series son I(1)
│
▼
┌─────────────────────────────────────────────────────────────────┐
│ PASO 5: PRIMERA DIFERENCIACIÓN (Retornos) │
│ rt = ln(Pt) - ln(Pt-1) ≈ Retorno % │
└────────────────────┬────────────────────────────────────────────┘
│
├─► ADF sobre retornos
├─► TODOS estacionarios (p < 0.01) [CORRECTO]
├─► Media constante (~0%)
├─► Volatilidad variable (clusters)
│
▼
**Conclusión:** ¡Retornos listos para modelado!
│
▼
┌─────────────────────────────────────────────────────────────────┐
│ PASO 6: ANÁLISIS ACF/PACF │
│ ¿Los retornos tienen estructura temporal? │
└────────────────────┬────────────────────────────────────────────┘
│
├─► Autocorrelaciones débiles
├─► Retornos ≈ ruido blanco
├─► Volatilidad SÍ autocorrelacionada
│
▼
**Conclusión:** Necesitamos modelos GARCH
│
▼
╔═════════════════════════════════════════════════════════════════╗
║ RESULTADO FINAL ║
║ ║
║ Serie transformada: RETORNOS LOGARÍTMICOS ║
║ Propiedades: ║
║ • Estacionarios I(0) [CONFIRMADO] ║
║ • Media constante [CONFIRMADO] ║
║ • Volatilidad variable (clusters) ║
║ • Colas pesadas (curtosis > 3) ║
║ ║
║ Listos para: ║
║ → Modelos ARIMA(p,0,q) ║
║ → Modelos GARCH para volatilidad ║
║ → Modelos de cambio de régimen ║
╚═════════════════════════════════════════════════════════════════╝2.5.3 Transformaciones Necesarias
| Variable | ¿Estacionaria? | Uso Recomendado |
|---|---|---|
| Precios (P_t) | NO | Visualización, descomposición |
| Log-Precios | NO | Análisis de tendencia, cálculo de retornos |
| Retornos (Primera Diferencia) | SÍ | Modelado ARMA, GARCH, pronóstico |
2.5.4 Justificación de Procedimientos
¿Por qué son necesarias estas transformaciones?
1. Descomposición de Series de Tiempo
La descomposición nos permitió identificar qué componentes (tendencia, estacionalidad, residuos) explican el comportamiento de los precios de acciones. El análisis reveló que la tendencia es el componente dominante, explicando más del 90% de la variabilidad en todas las series, mientras que la estacionalidad es prácticamente despreciable (menos del 5%). Este hallazgo es crucial porque confirma que, a diferencia de series económicas como ventas minoristas que presentan patrones estacionales predecibles, los precios accionarios no siguen ciclos mensuales o trimestrales fijos. Por lo tanto, en los modelos SARIMA que implementaremos en capítulos posteriores, no será necesario aplicar diferenciación estacional (D=0), simplificando significativamente la especificación del modelo y reduciendo el riesgo de sobre-parametrización.
2. Pruebas de Estacionariedad (ADF)
Las pruebas Aumentadas de Dickey-Fuller fueron fundamentales para confirmar que todas las series de precios en niveles son no estacionarias, presentando raíz unitaria con p-valores consistentemente superiores a 0.05. Esta no estacionariedad significa que la media y varianza de los precios cambian con el tiempo, violando el supuesto básico de los modelos ARIMA estándar. Sin esta confirmación estadística formal, podríamos haber intentado modelar directamente los precios, lo que habría resultado en regresiones espurias y pronósticos poco confiables. Las pruebas ADF nos permitieron determinar que las series son integradas de orden 1, es decir I(1), lo que indica que una sola diferenciación será suficiente para inducir estacionariedad. Este conocimiento guía directamente la especificación del parámetro d=1 en los modelos ARIMA(p,d,q) que desarrollaremos.
3. Transformación Logarítmica
Aplicamos la transformación logarítmica porque las series de precios de acciones presentan heterocedasticidad: cuando los precios son altos, las fluctuaciones absolutas también son mayores. Por ejemplo, una acción que vale $200 puede variar ±$10 en un día, mientras que cuando valía $20 solo variaba ±$1, pero ambas representan la misma variación porcentual del 5%. El logaritmo convierte este crecimiento multiplicativo en aditivo, estabilizando la varianza a lo largo del tiempo. Además, la transformación logarítmica tiene una ventaja interpretativa crucial en finanzas: la primera diferencia de log-precios es aproximadamente igual al retorno porcentual continuo, que es el estándar en finanzas cuantitativas. Esta interpretabilidad facilita tanto el análisis como la comunicación de resultados a stakeholders. Aunque la transformación log por sí sola no elimina la tendencia (las series log-transformadas siguen siendo no estacionarias), es un paso necesario antes de la diferenciación.
4. Primera Diferenciación (Cálculo de Retornos)
La diferenciación es la única transformación que logró inducir estacionariedad en nuestras series. Al calcular retornos logarítmicos como rt = ln(Pt) - ln(Pt-1), eliminamos la tendencia estocástica y obtuvimos series con media constante alrededor de 0% y propiedades estadísticas estables en el tiempo. Las pruebas ADF confirmaron que todas las series de retornos son estacionarias con p-valores < 0.01, lo que valida el uso de modelos ARMA y GARCH. Es importante destacar que aplicar una segunda diferenciación (d=2) sería contraproducente: generaría autocorrelación negativa artificial y complicaría innecesariamente el modelo. La regla fundamental en series de tiempo es usar el mínimo número de diferenciaciones necesarias para lograr estacionariedad. Por lo tanto, todos los modelos de pronóstico en capítulos posteriores trabajarán con retornos (d=0 sobre retornos ya diferenciados), no con precios en niveles, garantizando la validez estadística de nuestras inferencias y pronósticos.
2.5.5 Aplicaciones Futuras de los Hallazgos
Con base en los resultados de este capítulo, los siguientes modelos y técnicas serán apropiados para nuestros datos:
Modelado ARIMA: Dado que confirmamos que los retornos son estacionarios I(0) con autocorrelaciones débiles, podemos especificar modelos ARIMA(p,0,q) para capturar cualquier estructura lineal residual en la media condicional. El orden p (autorregresivo) y q (media móvil) se determinará mediante los criterios AIC/BIC, aunque anticipamos valores bajos (p,q ≤ 2) dado que los retornos se aproximan a ruido blanco.
Modelado GARCH: El análisis reveló clusters de volatilidad evidentes, especialmente durante el periodo COVID-19 en marzo 2020, donde los retornos diarios alcanzaron ±30%. Aunque los retornos mismos tienen poca autocorrelación, los cuadrados de los retornos (proxy de volatilidad) sí presentan fuerte autocorrelación. Esto justifica el uso de modelos GARCH(p,q) o EGARCH para capturar la heterocedasticidad condicional y modelar la volatilidad variable en el tiempo, crucial para gestión de riesgo y valoración de derivados.
Modelos de Cambio de Régimen: El análisis de descomposición identificó quiebres estructurales claros durante COVID-19 en todas las series, con cambios dramáticos en los niveles de precios y volatilidad. Además, Moderna (MRNA) experimentó un cambio de régimen extremo con el desarrollo de vacunas. Estos patrones sugieren que modelos Markov-Switching o modelos con variables dummy para eventos discretos podrían capturar mejor la dinámica que modelos lineales estándar. Estos enfoques nos permitirán identificar y modelar diferentes regímenes de mercado (alta volatilidad vs. baja volatilidad, tendencia alcista vs. bajista).
Análisis de Distribuciones No-Normales: Las estadísticas descriptivas mostraron que todos los activos presentan curtosis >3 (colas pesadas) y asimetría negativa, indicando mayor probabilidad de caídas extremas que lo que predeciría una distribución normal. Al estimar modelos GARCH, consideraremos distribuciones alternativas para los errores, como la t de Student o distribuciones skewed, que capturan mejor estos eventos extremos y mejorarán la precisión de intervalos de confianza y medidas de riesgo como Value-at-Risk (VaR).
Integración con Black-Scholes: La volatilidad estimada mediante modelos GARCH puede alimentar directamente el modelo de Black-Scholes para valoración de opciones, reemplazando el supuesto de volatilidad constante por una estimación dinámica más realista. Esto permitirá pricing más preciso de opciones y estrategias de cobertura más efectivas, conectando el análisis de series de tiempo con aplicaciones prácticas en mercados de derivados.